こんにちは、ギガンくず(@gigankuzu69)です。
モンハンライズには「20%の確率で弾を消費せずに撃てる」という効果の弾丸節約というスキルがあります。
ところがこのスキル20%以上、具体的には25%で発動しているとの噂があり、僕も時々目にしたことはあったのですが「ほんまかいな」ぐらいにしか思ってなかったのでちょっと検証してみる事にしました。
というのも装填拡張と弾丸節約の記事に頂いたコメントがきっかけです。
検証方法
修練場のカカシに向かって通常弾Lv3を撃ち、弾丸節約が発動する回数をカウントする。
というシンプルな方法で調べてみたいと思います。
具体的な方法としては連射コントローラーを使い、修練場のカカシに自動で弾を撃っている所を録画します。その録画を見て数取器で弾丸節約の発動回数をカウントしていきます。
 なんとアナログな・・・
なんとアナログな・・・検証結果
修練場のヒット数のカウント上限が999hitまでなので3回に分けて計2485発分計測しましたが、いずれも20%を大きく上回って25%~26%の間になりました。
1回目 999回射撃中267回発動

2回目 999回射撃中260回発動

3回目 487射撃中125回発動
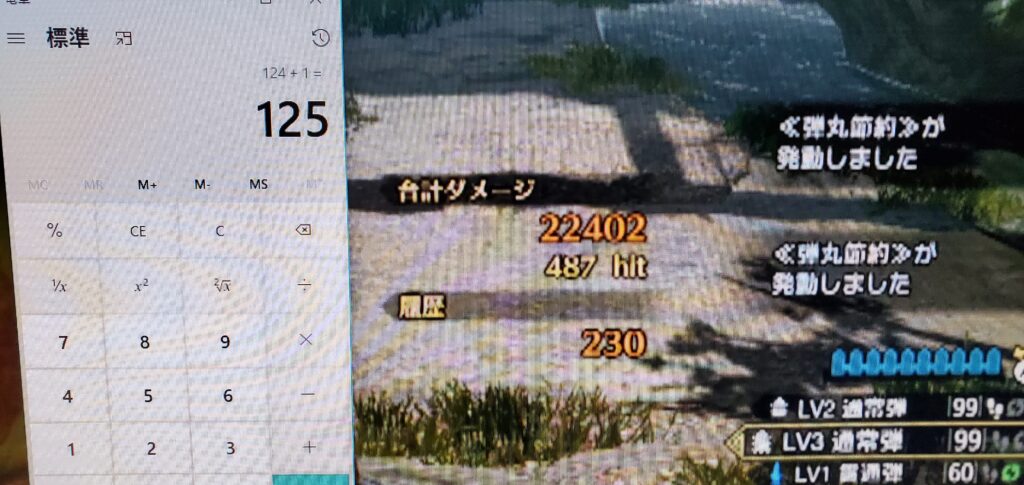 (手動でカウントが思ったよりめんどかったので自動化しました。)
(手動でカウントが思ったよりめんどかったので自動化しました。)
合計2485射撃中652回発動=約26.2%
回数が少ないので噂されている25%より少し高くなりましたが、少なくとも20%よりは発動していますね。
つまりやっぱり弾丸節約の発動確率は20%ではないという事なのでしょうか。
追記:コメント欄にかなり詳しく検証結果を書いていただきました。正直コメント欄がこの記事のメインコンテンツです。皆様本当にありがとうございます。
コメント欄にもあるように結論としては「弾丸節約の発動確率は25%である」という事でよさそう?
とりあえず僕の考え方を書いた所は暫定的に折り畳みにしました。
※以下の情報は僕が足りない知識で考えたものなので必ずしも正しいとは限りません。
旧内容
と、思ったのですが「弾丸節約 期待値」で検索している時にすごく詳しく書いてあるページがありました。
MHW:IBの頃の記事ですが、弾丸節約の期待値について数学的にめっちゃ詳しく書いてありすごいタメになります。是非ご一読ください。
僕には数学の知識が無いので記事をお借りします。
こちらのnoteの中に
弾丸節約スキルあり・弾丸節約の効果が20%の確率で発生すると仮定したときの「1発の弾で撃てる見込み弾数」でしたね。結論としては、見込み弾数EはE=1.25となります。
ttps://note.com/kuaty8944/n/nf87f503c4de9
という記載があります。
つまり弾丸節約が20%だと実際に撃てる弾の数は25%増えるって事ですよね。
増えた弾の数=ゲーム画面上の弾丸節約発動ログとしたら、25%分発動ログがあるって事は弾丸節約の確率は20%って事になるんですかね。
なんだかよく分からなくなってきました。が、個人的には「弾丸節約の発動確率が20%なので撃てる弾は25%増えるため弾丸節約の発動ログも25%になる」というのがなんかしっくりくるような気がするんですがどうでしょうか。
有識者の皆様いかがでしょうか。

そうですね!弾丸節約と装填拡張の記事も前提条件を変えて追記したいと思います!
となるとよっぽど装填数低いヘビィを使いたい!ってわけでもない限り大体弾丸節約で良さそうになりますね~
皆様コメントで色々教えていただきありがとうございます!
僕の知識が足りないばかりに皆様にご協力いただき申し訳ありません🙇♂️
正直よく分かってないまま見切り発車で投稿したのでもっと叩かれるかと思ってたんですが、優しいインターネットで安心しました笑
本当にありがとうございます😭
しかし、発動が25%となると前回の記事だった火力面での弾丸節約の貢献度もまた変動しそうですよね。次回を期待!ということで良いですか?笑
こっちでも計算してみましたが
装填数3の時に装填拡張=弾丸節約
装填数4以上の時は装填拡張よりも弾丸節約の方が強い
って結果になりましたね
節約の記事にコメントさせて頂いた者です。
さっそく新しい記事をありがとうございます。
>>つまり弾丸節約が20%だと実際に撃てる弾の数は25%増えるって事ですよね。
>>増えた弾の数=ゲーム画面上の弾丸節約発動ログとしたら、
この部分は正しいと思います。
>>25%分発動ログがあるって事は弾丸節約の確率は20%って事になるんですかね。
ここが間違っているのではないでしょうか?
例えば、2回目の実験では、999回射撃して260回発動していますが、
「999」は射撃した弾の数です。
つまり、「元々用意した弾+節約で増えた弾」の合計が999です。
元々用意していた弾の数(=消費した弾の数)は
999-260=739発だと考えられます。
「739発用意して射撃したら、節約で260発増えて、999発撃てた。」
というのが2回目の実験結果であり、
発動ログの割合は、260÷739 = 35.18%
見込み弾数EはE= 999÷739 = 1.3518
こうなるのではないでしょうか?
「撃った弾の25%」と「用意した弾の25%」
これらは別々のものである事に注意して計算する必要があると思います。
長くなってしまったので分割
あと、リンクが貼ってある記事のように難しく考えるのではなく、
弾丸節約が発動率20%なら
1発撃つたびに(100%-20%)=80%の確率で弾を1個消費
=1発撃つたびに弾を0.8個消費する と期待値は同じ。
弾を100個用意したら 0.8個づつ消費するので、
100÷0.8=125回射撃できる。(E=1.25)
弾丸節約が発動率25%なら
1発撃つたびに(100%-25%)=75%の確率で弾を1個消費
=1発撃つたびに弾を0.75個消費する と期待値は同じ。
弾を100個用意したら 0.75個づつ消費するので、
100÷0.75=133.3回射撃できる。(E=1.333)
今回の実験結果では
合計2485射撃中652回発動だった。(=1833個の弾丸を消費した。)
射撃1回につき平均で何個の弾丸を消費したかというと
1833/2485 ≒ 0.74個
→1発撃つたびに0.75個消費する「節約発動率25%」
と近い結果になった。
こんな風に
発動率○○% = 1回射撃ごとに弾を☓☓個消費する(期待値は同じ)
って感じで考えた方が計算が簡単になるのではないかと思います。
コメントありがとうございます!
かなり分かりやすいですね笑
僕に学が無いのでなんとか理解しようと難しく考えすぎてたのかもしれません🤔
こんな場末のブログに色々お時間使っていただいて本当にありがとうございます!
≫ 発動ログの割合は、260÷739 = 35.18%
この部分だけは違うんじゃないですかね?分子となる260の中にも、弾丸節約によって増えた弾に対し発動した回数が含まれており、元々用意していた弾739内で発動した分以上がカウントされているのかと思われます。
>>元々用意していた弾739内で発動した分以上がカウントされている
これはその通りなのですが、
今回はその発動した分以上カウントするのが正しい計算になると思われます。
こちらの記事では、弾丸節約が20%の時の理論上の数値として
リンク先の記事からデータ引用されており、その記事では、
「1発の弾で撃てる見込み弾数」=「用意した弾の数を撃ち切った時の発動割合」
を計算して求めています。(E=1.25 とか。)
つまり、
「リンク先の理論上の数値」と「今回の実験結果」を比較するためには、
こちらの実験結果も
「1発の弾で撃てる見込み弾数」=「用意した弾の数を撃ち切った時の発動割合」
を計算して求める必要があります。
要するに、リンク先の理論データが
そういう(違うんじゃない?って思えるような)計算をしているので、
こちらもそういう計算をしないと正しい比較にならない、
というのが、260÷739 = 35.18% (E=1.35)の計算をしている理由です。
失礼します。
検証に連射パットを使用されたとのことですが、正確な発動確率となると例えば装填数10の武器なら10発全部撃ちきるのではなく、弾丸節約が3回発動したら3発分を残してリロード→繰り返し。と手動でやらなければ、スキルが発動した際に弾が減らないという弾丸節約の特性上、正確な発動確率ではないかと思います…。
大変失礼致しました。実際のところどうなんだろうなと興味が湧き自分でも調べてみました。間違っていたらすいません、ご了承願います。
まずあくまで今回は「弾丸節約の(1発ごとの)発動確率は本当に20%か」という検証だったと思われますのでそこに沿って見てみました。
①例として1000発撃ち込んだ際、表記どおりの発動確率20%であれば、その内訳は約800が消費する弾(消費弾)、約200がスキルによって生み出された弾(スキル弾)ということになります。この場合、スキル弾は全体1000発の20%で消費弾の0.25倍。消費弾の1.25倍が=全体1000(見込み弾)です。
②同様に1000発撃ち込む際、前提を発動確率25%の場合で考えてみると、消費弾は約750、スキル弾は約250ということになります。その場合だとスキル弾は全体1000の25%で消費弾の0.3333…倍、消費弾の1.3333…倍が=全体1000(見込み弾)となります。
では、今回主さまが実際に検証された数字を当て込むと、1000発(999発)撃ち込んだ際のスキル弾は267と260ということなので、消費弾がそれぞれ733と740。3回目のスキル弾も250は順当に超えそうなため、弾丸節約1発ごとのスキル発動率は②にかなり近い検証結果なのかと思います。見込み弾はそれぞれの消費弾の1.36425…倍、1.35135…倍ですかね?これも②に近いですね。
なので今作の弾丸節約3の発動確率は25%前後が正しいように思います。
検証ありがとうございます!
正直僕も手探りでやってみただけなので、僕の出した結果から考えをまとめて頂けるの助かります🙇♂️
何より複数人で同じ目的を持って検証している感じが上手く言えないですけど楽しくて好きですね笑